In part 3 we’ll introduce some of the math behind qubits.
Note: this post is part of my series, Programming the Multiverse
More on the H gate
Last time, we introduced some basic gates, including the H gate. We saw that the H gate puts a qubit into a Superposition where it has a 50% chance of being a \(\ket{0}\) or a 50% chance of being a \(\ket{1}\) when measured.
What happens if we combine two H gates?
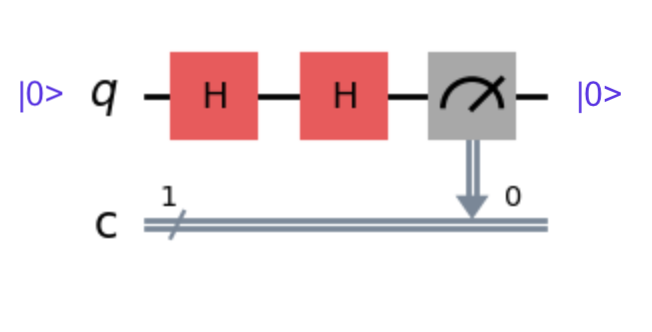
If we input a qubit set to \(\ket{0}\) through the two H gates, we get… a \(\ket{0}\)! Likewise, if we input a qubit set to \(\ket{1}\) we get a \(\ket{1}\).
What’s going on? Here’s where we have to finally delve into a little bit of math.
It’s all probability
The most important thing to remember is that qbits are never really representing actual data values, but they represent probabilities of seeing a 0 or a 1. And the gates are just manipulating those probabilities.
When we say a qubit is \(\ket{0}\) or \(\ket{1}\) what we’re saying is there’s a 100% probability of seeing a 0 or a 1.
Every qubit can be described by a formula:
\[\ket{\psi} = a\ket{0} + b\ket{1}\]If you recall, we pronounce it “ket-zero” and “ket-one.” Here we’re using Bra-Ket Notation. No, this does not have anything to do with anesthesia and intimate apparel, it’s just signifying that we’re talking about vectors (more on that later). It’s also called Dirac Notation.
The variables a and b are called the Probability Amplitude. The way this formula works is that a and b have to add up, such that \(\vert{a}\vert^{2} + \vert{b}\vert^{2} = 1\). So in this formula, the total probability is 1 (100%) and the squares of the probabilities, a and b add up to 1.
In the case of a qubit that is definitely 0, we have \(1\ket{0} + 0\ket{1}\). We can drop the \(\ket{1}\) since it’s multiplied by 0. Similarly, a definite 1 is \(0\ket{0} + 1\ket{1}\) which simplifies to \(\ket{1}\).
For a qubit that is in superposition, we have a 50% chance of a 0 or a 1. So if we solve backward from:
\[\vert{a}\vert^{2} + \vert{b}\vert^{2} = 1\]and get:
\[\vert{\sqrt{\frac{1}{2}}}\vert^{2} + \vert{\sqrt{\frac{1}{2}}}\vert^{2} = 1\]So that the squares cancel out the square roots:
\[\frac{1}{2} + \frac{1}{2} = 1\]So then a and b are both equal to \(\sqrt{\frac{1}{2}}\) which simplifies to \(\frac{1}{\sqrt{2}}\).
Our final state vector is: \(\ket{\psi} = \frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}\ket{1}\)
If we had a 25% chance of 0 and a 75% chance of 1, it would be \(\ket{\psi} = \frac{1}{\sqrt{4}}\ket{0} + \frac{\sqrt{3}}{\sqrt{4}}\ket{1}\)
Back to the H gate
So the H gate is doing something to manipulate those probability amplitudes, a and b. But How? And how does it move each one from 0% or 100% to 50%? Stay tuned for Part 4.
Next article: Part 4 - The Guts of Gates